A Dirichlet-distributed random variable can be seen as a multivariate generalization of a Beta distribution.
Dirichlet 分布随机变量可视为 Beta 分布的多变量广义化.
reference: https://towardsdatascience.com/dirichlet-distribution-a82ab942a879
A few months ago, I built a recommender system that employed topic modelling to display relevant tasks to employees. The algorithm used was Latent Dirichlet Allocation (LDA), a generative model that has been around since the early 2000s¹. Of course, I didn’t rewrite LDA from scratch but used the implementation in Python’s scikit-learn. But it started me thinking about the sequence of research that lead to the creation of the LDA model. The problem with such libraries is that it’s all too easy to include a few lines in your code and just move on, so I dug out my old machine learning books with the goal of knowing enough to be able to explain LDA in all its gory probabilistic detail. At one point there was a worry that it would turn into an infinite regression, but in the end reason prevailed, and this sequence of articles was constructed. In reverse order, we have:
V: Latent Dirichlet Allocation (LDA)
IV: Latent Semantic Indexing (LSA)
III: Mixture models and the EM algorithm
II: Bayesian generative models
I: Dirichlet distribution
Hopefully by the time we get to the end the aim would have been achieved. We shall start with the Dirichlet distribution.
Dirichlet distribution — what is it, and why is it useful?
Looking up the Dirichlet distribution in any textbook and we encounter the following definition:
The Dirichlet distribution Dir(α) is a family of continuous multivariate probability distributions parameterized by a vector α of positive reals. It is a multivariate generalisation of the Beta distribution. Dirichlet distributions are commonly used as prior distributions in Bayesian statistics.
An immediate question is why is the Dirichlet distribution used as a prior distribution in Bayesian statistics? One reason is that it is the conjugate prior to a number of important probability distributions: the categorical distribution and the multinomial distribution. Using it as a prior makes the maths a lot easier.
Conjugate prior
In Bayesian probability theory, if the posterior distribution p(θ|x) and the prior distribution p(θ) are from the same probability distribution family, then the prior and posterior are called conjugate distributions, and the prior is the conjugate prior for the likelihood function.
If we think about the problem of inferring the parameter θ for a distribution from a given set of data x, then Bayes’ theorem says that the posterior distribution is equal to the product of the likelihood function θ → p(x|θ) and the prior p(θ), normalised by the probability of the data p(x):

Since the likelihood function is usually defined from the data generating process, we can see that the difference choices of prior can make the integral more or less difficult to calculate. If the prior has the same algebraic form as the likelihood, then often we can obtain a closed-form expression for the posterior, avoiding the need of numerical integration.
Motivating the Dirichlet distribution: dice manufacturing
We show how the Dirichlet distribution can be used to characterise the random variability of a multinomial distribution. I’ve borrowed this example from a great blog post on visualising the Dirichlet distribution.
Suppose we are going to manufacture 6-sided dice but allow the outcomes of a toss to be only 1, 2 or 3 (this is so the later visualisation is easier). If the die is fair then the probabilities of the three outcomes will be the same and equal to 1/3. We can represent the probabilities for the outcomes as a vector θ =(θ₁, θ₂, θ₃).
θ has two important properties: first, the sum of the probabilities for each entry must equal one, and none of the probabilities can be negative. When these conditions hold, then the results associated with rolling of the die can be described by a multinomial distribution.
In other words, if we observe n dice rolls, D={x₁,…,x_k}, then the likelihood function has the form
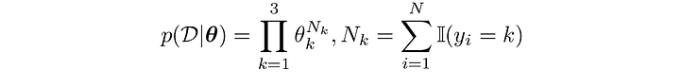
Where N_k is the number of times the value k∈{1, 2, 3} has occurred.
We expect there will be some variability in the characteristics of the dice we produce, so even if we try to produce fair dice, we won’t expect the probabilities of each outcome for a particular die will be exactly 1/3, due to variability in the production process. To characterise this variability mathematically, we would like to know the probability density of every possible value of θ for a given manufacturing process. To do this, let’s consider each element of θ as being an independent variable. That is, for θ =(θ₁, θ₂, θ₃), we can treat θ₁, θ₂ and θ₃ each as an independent variable. Since the multinomial distribution requires that these three variables sum to 1, we know that the allowable values of θ are confined to a plane. Furthermore, since each value θᵢ must be greater than or equal to zero, the set of all allowable values of θ is confined to a triangle.
What we want to know is the probability density at each point on this triangle. This is where the Dirichlet distribution can help us: we can use it as the prior for the multinomial distribution.
Dirichlet distribution
The Dirichlet distribution defines a probability density for a vector valued input having the same characteristics as our multinomial parameter θ. It has support (the set of points where it has non-zero values) over

where K is the number of variables. Its probability density function has the following form:

The Dirichlet distribution is parameterised by the vector α, which has the same number of elements K as our multinomial parameter θ. So you can interpret p(θ|α) as answering the question “what is the probability density associated with multinomial distribution θ, given that our Dirichlet distribution has parameter α.”
Visualising the Dirichlet distribution
We see the Dirichlet distribution indeed has the same form as the multinomial likelihood distribution. But what does it actually look like?
To see this we need to note that it is the multivariate generalisation of the beta distribution. The beta distribution is defined on the interval [0, 1] parameterised by two positive shape parameters α and β. As might be expected, they are the conjugate priors for the binomial (including Bernoulli) distributions. The figure shows the probability density function for the Beta distribution with a number of α and β values.

As we can see, the beta density function can take a wide variety of different shapes depending on α and β. When both α and β are less than 1, the distribution is U-shaped. In the limit of α = β → 0, it is a 2-point Bernoulli distribution with equal probability 1/2 at each Dirac delta function ends x=0 and x=1, and zero probability everywhere else. When α=β=1 we have the uniform [0, 1] distribution, which is the distribution with the largest entropy. When both α and β are greater than 1 the distribution is unimodal. This diversity of shapes by varying only two parameters makes it particularly useful for modelling actual measurements.
For the Dirichlet distribution Dir(α) we generalise these shapes to a K simplex. For K=3, visualising the distribution requires us to do the following: 1. Generate a set of x-y coordinates over our triangle, 2. Map the x-y coordinates to the 2-simplex coordinate space, 3. Compute Dir(α) for each point. Below are some examples, you can find the code in my Github repository.

We see it is now the parameter α that governs the shapes of the distribution. In particular the sum α₀=∑αᵢ controls the strength of the distribution (how peaked it is). If αᵢ < 1 for all i, we get ‘spikes’ at the corners of the simplex. For values of αᵢ > 1, the distribution tends toward the centre of the simplex. As α₀ increases, the distribution becomes more tightly concentrated around the centre of the simplex.
In the context of our original dice experiment, we would produce consistently fair dice as αᵢ → ∞. For a symmetric Dirichlet distribution with αᵢ > 1, we will produce a fair dice, on average. If the goal is to produce loaded dice (e.g. with a higher probability of rolling a 3), we would want an asymmetric Dirichlet distribution with a higher value for α₃.
We now have seen what the Dirichlet distribution is, what it looks like and the implications of using it as a prior for a multinomial likelihood function in the context of a dice-manufacturing example. In the next post we’ll dive into Bayesian generative models and how to perform inference.
usage
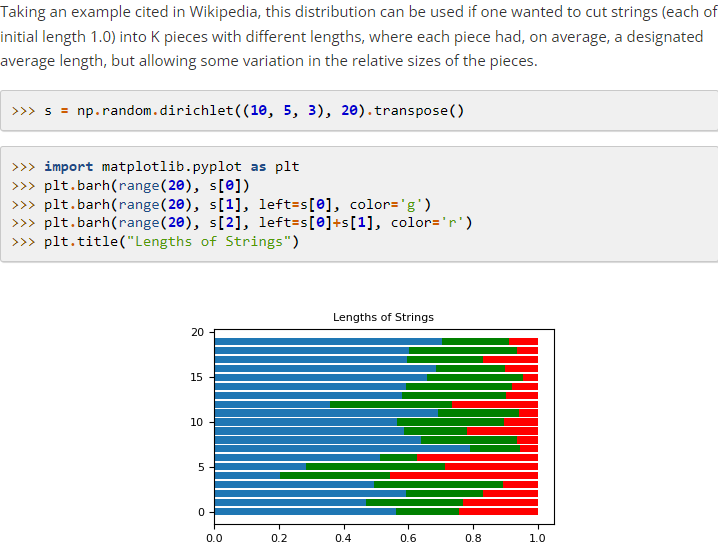
import numpy as np
min_size, min_require_size = 0, 10
n_parties = 10
K = 10 # class num
y_train=np.array([_ for _ in range(10)]*10)
np.random.shuffle(y_train)
beta = 1 # the dirichlet distribution
N = len(y_train)
while min_size < min_require_size:
idx_batch = [[] for _ in range(n_parties)]
for k in range(K):
idx_k = np.where(y_train == k)[0]
np.random.shuffle(idx_k)
proportions = np.random.dirichlet(np.repeat(beta, n_parties))
## Balance
proportions = np.array([p * (len(idx_j) < N / n_parties) for p, idx_j in zip(proportions, idx_batch)])
proportions = proportions / proportions.sum()
proportions = (np.cumsum(proportions) * len(idx_k)).astype(int)[:-1]
idx_batch = [idx_j + idx.tolist() for idx_j, idx in zip(idx_batch, np.split(idx_k, proportions))]
min_size = min([len(idx_j) for idx_j in idx_batch])
print(idx_batch)

